Peter Rosati, Russell K. Dean, Member, IEEE, and Susan M. Rodman
IEEE Transactions On Education, Vol. 31 No. 3, August 1988
Abstract - The Myers-Briggs type indicator (MBTI) has been used by previous researchers as an indicator of the learning style preferences of engineering students in problem-solving courses. In particular, the intuitive/sensing scale separates intuitive students with a preference for abstract, global, and theoretical approaches from the sensing students with their preference for the practical, factual, and specific approach. This paper describes an experiment in which separate teaching presentation modes were designed - one sensing and the other intuitive - and presented to two similar groups of engineering students. The interactions between student learning style, teaching presentation mode, and student performance are explored.
The Myers-Briggs Type indicator (MBTI) was devised to represent Jung's theory 1 of psychological structure concerning the way people perceive information and make judgments. Form G of the indicator consists of 166 forced-choice items and categorizes the respondent on four dichotomous scales: extraversion/introversion (E/I), sensing/intuition (S/N), judgment/perception (J/P) and thinking/feeling (T/F). The MBTI type is expressed as a combination of the four scales, such as ISFJ or ENTP, and it reflects the respondent's favored style of perceiving and judging in all situations including the learning situation.
Most of the studies concerning the MBTI type and learning style have focused separately on one of the four MBTI scales. 2 The perception functions (S or N) are relevant to the learning setting and describe how information is internalized, either through the senses (S) or through intuition (N ). McCaulley 3 states that the psychological theory behind the MBTI would predict the sensing types (the "S's" ), in their learning, rely on experience rather than theory and have a preference for moving from the known in a step-by-step manner. Intuitive types (the ''N's" ), on the other hand, rely more on intuition and inspiration which often leads to an ability to understand abstract, symbolic, and theoretical relationships.
Several researchers have considered the learning process in relation to the S/N dimension of the MBTI. Eggins 4 addressed the interaction between the structure of learning materials and the personality type of learners. She designed three models for teaching sixth graders a science concept: a highly structured Gagné model, an inductive Bruner model, and Ausubel's advance organizer model followed by a didactic lesson. There was no significant interaction between the MBTI S/N scale and the student performance scores either on the immediate post-test or on the delayed (ten days) post-test. For students in the extreme groups of the field dependence/field independence range, however, the N students learned more with the Bruner model. The S students, if field independent, learned best with the Ausubel model. Also, it was found that for students in the lower half of the crystallized intelligence range, the NP students performed significantly better when taught by the Brunner model. Eggins concluded that the need for an appropriate match between student type and teaching style is more critical for students of below average intelligence.
Irey, 5 working with university engineering students, wrote a 20 unit PSI. course in thermodynamics and was able, with some confidence, to categorize 18 of these units as written in an S style (containing detailed routine work with practical applications) or in an N style (which focused more on concepts, new problems, and ideas). He then correlated the student's preference for the unit with the student's MBTI type on the S/N scale. In the majority of cases, the S students preferred the S style units and the N students preferred the N style units. Irey used the z test to determine whether he had accurately predicted the students' ratings of the course units and found his results significant at the 0.01 level.
Yokomoto and Ware 6 administered the MBTI to students in electrical engineering courses over a two-year period and conducted interviews about their learning strategies. They found that in courses where the examination problems were similar to the homework problems, the correlation of the scores of the S students between homework problems and exam problems was higher than the correlation for the N students. If, however, the examinations contained conceptual problems different from the homework, this result was reversed and the N students' scores correlated higher. A third group of students was coached in their nonfavored behavior, i.e., the S types were coached in extracting principles and concepts from their many worked examples, whereas the N types were encouraged to practice more routine solutions. For this group of coached students, the correlation between homework and examination scores was approximately the same for N students as for S students even when conceptual problems were included in the examinations.
This investigation examined the interaction of learning style and the presentation modes of material in part of a mechanics of materials engineering course. The students completed the MBTI, were divided into two groups, and exposed to parallel but different presentation modes of course material. The first presentation mode was designed to appeal to the S type and the second to appeal to the N type. All students were evaluated on common examinations which were designed to contain both "S type" and "N type" questions.
The experiment took place within a junior level mechanics of materials course at West Virginia University in the Fall of 1984. A discrete 9 hour topic on "forces and stresses in beams" was selected for instruction by each of the two presentation modes, one a theoretical "N style" and the other an algorithmic "S style.''
The MBTI was administered to the 31 students in the course and the subjects were assigned to treatment groups according to their scores on the S/N continuum. The resulting groups were nearly identical in terms of both type and score on the S/N dimension.
One group was taught by an INFJ instructor in a theoretical "N style" manner. Emphasis was placed on derivations, concepts, and theoretical treatments with extrapolations to concepts of similar mathematical type, and the in-class worked examples emphasized the algebraic approach.
The other group was taught by an ISTJ instructor in a step-by-step algorithmic "S style" treatment that emphasized details and used numerical rather than algebraic in-class examples. Both groups were given the same homework problems, but they were not collected for grading. identical solution sheets were distributed to both groups.
The students wrote a common one hour examination at the end of the experimental period. It consisted of ten multiple-choice questions and three problems. Half of the questions were designed as conceptual "N type " questions and half as algorithmic "S type" questions. The final examination' two weeks later (at the end of the course), consisted of nine problems, three of which related to the "bending" topics covered in the experimental teaching treatments.
A questionnaire was designed to determine how the students in each treatment felt about the instructional mode.
The questionnaire was specifically used to assess how well the students' learning style matched the instructors' teaching style, how students perceived the usefulness of both lectures and texts, and how the students generally felt about the effectiveness of their instructor's teaching style.
At the end of the treatment period, a questionnaire was distributed to both groups which inquired as to their perceptions about the instructional treatments they had received. The questionnaire items and the average response for each treatment group are indicated in Table I. The results show the average response for "S's" and "N's" for each treatment group. Several interesting trends emerged from that data.
For items 3 and 6, students were requested to respond using a Likert-type scale with "1" indicating strong agreement with the statement and "5" indicating strong disagreement. For both items, all students showed a strong preference for the S type teaching strategy.
Items 2 and 5 attempted to ascertain whether students depended primarily upon the text or lecture presentation for gathering information and forming concepts during the treatment period. The same Likert-type scale was again employed. The results indicate that for these particular students the textbook did not serve as a major source of information. It therefore appears that the information received by students within this unit of the mechanics of materials course was primarily of an S or N orientation, depending upon the student's group assignment.
Item 7 seems to confirm the validity of the design of the teaching styles used by the two instructors. Students did, in fact, perceive an S treatment as algorithmic and detailed and the N treatment as conceptual and abstract. This lends credence to the originally stated intention of the investigators.
Finally, items 8, 9, and 10 asked students to rate the teaching abilities of their respective instructors. Had one instructor been perceived as a poor teacher, this would have seriously biased all resulting data. Both instructors were rated as well above the average. Teaching ability does not appear to be a confounding variable for these data.
An hour examination was administered following the experimental treatment (i.e., the unit on "bending"). That examination consisted of two parts: 1) ten multiple choice questions, each worth four points and 2) three computational problems, each worth 20 points. Multiple choice questions were designed to address either broad underlying concepts (''N'' questions) or specific applications ("S" questions). Computational problems were purely algorithmic and were not intended to favor either strategy.
This testing format allowed three separate comparisons to be explored: 1) differences on S type questions, 2) differences on N type questions, and 3) differences on computational problems. Group and subgroup means appear in Tables II and III.
All comparisons were evaluated by means of analysis of covariance using the GLM procedure within the statistical analysis system (SAS) version 82.4 and an IBM 3081D mainframe computer. In all cases the S-N classification of the student and teaching mode (S versus N) constituted main effects and grade point average (GPA) served as the covariate. Results of these analyses appear in Table IV.
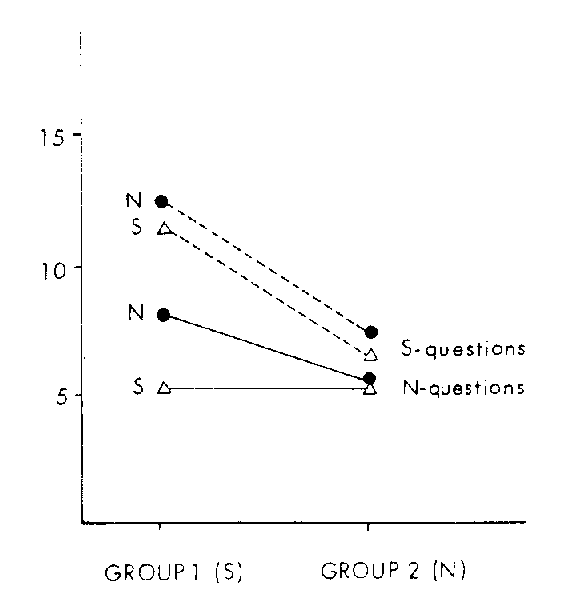
Analysis of performance on S type multiple choice questions revealed no significant differences due to personality classification. A highly significant difference emerged in regards to teaching mode. Students receiving detailed, algorithmic instruction ( i. e., the " S" treatment) performed substantially better on "S" oriented questions. In addition, there was a small but significant interaction between personality type and instructional mode, as shown in Figure 1.

It appears that N students performed much better in an "S" environment than S students given N type instruction.
No meaningful differences were detected regarding performance on N type questions. Students of both personality types answered these questions with equal competence. Likewise, there were no differences due to instructional mode and no interaction of main effects.
| Item | Group 1 ("S" Treatment) n = 11 | Group 2 ("N" Treatment) n = 12 |
| 1 I thought the lectures were very helpful. (1 agree - 5 disagree) | 1.84 |
2.16 |
| 2 The concepts I formed about bending came from the text rather than from the lectures. (1 agree - 5 disagree) | 4.07 |
3.75 |
| 3 The instructor's teaching style was similar to my learning style. (1 agree - 5 disagree) | 1.92 |
3.49 |
| 4 My instructor spent too much tine on details. I would have preferred more discussion of concepts and ideas. (1 agree - 5 disagree) | 4.00 |
4.16 |
| 5 For this section of the course, the text was more helpful than the lectures. (1 agree -5 disagree) | 4.30 |
3.66 |
| 6 My instructor spent too much tine on concepts and mathematical relations and not enough on practical applications and numerical examples. (1 agree - 5 disagree) | 4.00 |
2.41 |
| 7 Would you rate this instructor's emphasis as (1) conceptual and general, or (5) numerical and specific examples. (1 conceptual - 5 specific) | 4.36 |
1.74 |
| 8 Overall how would you rate your instructor's teaching style. (1 good - 5 poor ) | 1.15 |
2.07 |
| 9 How would you rate your instructor's ability to explain things. (1 good - 5 poor) | 1.23 |
1.58 |
| 10 Rate this instructor with others you have had in college. (1 best - 5 worst) | 1.53 |
2.25 |
| S-Students | N-Students | |||||
| S-Questions | N-Questions | Total | S-Questions | N-Questions | Total | |
| Group 1 "S" Treatment | 11.52 |
5.32 |
16.88 |
12.00 |
8.00 |
20.00 |
| Group 2 "N" Treatment | 6.2 |
5.32 |
11.52 |
7.32 |
6.00 |
13.32 |
| S-Students | N-Students | |
| Group 1 "S" Treatment | 37.11 |
39.00 |
| Group 2 "N" Treatment | 33.00 |
33.66 |
| Dependent Variable | Comparison | F | P > F |
| S-Type Questions: | Student Learning Style (S vs N) | 1.67 | .2047 |
| Teaching Style (S vs N) | 10.68 | .0038 *** | |
| Learning Style X Teaching Style | 3.74 | .0279 ** | |
| N-Type Questions: | Student Learning Style (S vs N) | .40 | .7572 |
| Teaching Style (S vs N) | .15 | .7004 | |
| Learning Style X Teaching Style | .82 | .4973 | |
| Problems: | Student Learning Style (S vs N) | .60 | .6235 |
| Teaching Style (S vs N) | .40 | .5338 | |
| Learning Style X Teaching Style | 2.61 | .0800 * |
Table IV. Tests For Significant Differences Between Teaching Styles, Learning Styles, And Their Interaction On The Hour Examination
* Sig a = .10 --- ** Sig a = .05 --- *** Sig a = .01
A similar pattern emerged regarding ability to solve computational problems. F values obtained for both main effects and for their interaction failed to achieve significance.
The final examination consisted of six algorithmic problems. The examination was written by a committee which included neither instructor. Three of the exam problems pertained to material covered during the experimental treatment (the unit on bending). 5 and N students from both groups could therefore be compared on three separate parameters: bending problems, nonbending problems, and total examination score. Means appear in Table V.
Two-way analysis of convariance was again performed using the same methods as applied to the hour test. Results of these analyses appear in Table VI.
In regard to nonbending problems and to the final examination as a whole, no significant differences were detected. For those problems relevant to the experimental treatment, however, the pattern was strikingly different. Main effects for personality type and teaching mode reached significance beyond the 5 percent level. N students and S students in Group 1 (the "S" treatment) achieved significantly higher scores. In addition, a significant interaction of these effects was found and is presented graphically in Figure. 2.
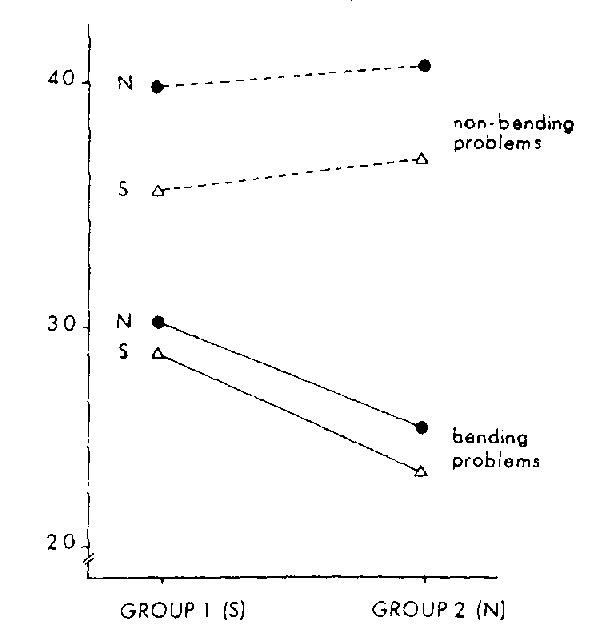
As in the case of the hour examination, N students fared better under an 5 instructional mode than did S students given a more conceptual presentation.
This investigation explored an aptitude-treatment interaction between the sensing-intuitive dimension of the MBTI and two methods of presenting the same information in an undergraduate engineering course. Based on the experience of Yokomoto and Ware, 6 the authors had expected students of differing S-N preferences to perform differently under the two methods of instruction. In addition, students were expected to express a preference for the teaching method which coincided with their particular MBTI classification.
Presentation mode does seem to affect performance, but in more subtle and complex ways than had been anticipated. A possible explanation lies in the academic histories of the students. In the typical engineering curriculum, they have been required to become extremely proficient at the solution of complex mathematical algorithms with little testing emphasis given to the conceptual basis of those algorithms. They have learned from experience that success on tests requires mastery of mathematical skills, but seldom depends on an understanding of physical principles and abstract relationships. For the S student, this is congruent with his natural inclinations. The N student, however, has been forced to adapt. In so doing, he may have become a stronger student, one who feels at home with both conceptual and practical material. The results of this investigation seem to support such an hypothesis. The performance of N students was superior in all cases. Differences continued to exist even after statistically adjusting for GPA. In the case of the final examination, N students scored significantly better than their S counterparts in regards to material covered during the experimental period. N. students, it appears, were better able to adapt to a different teaching style than were the S. who had always operated in a familiar mode.
| Group 1 (S-Treatment) | Group 2 (N-Treatment) | |||
| S-Students | N-Students | S-Students | N-Students | |
| Bending Problems | 29.6 |
30.0 |
22.88 |
25.5 |
| Non-Bending Problems | 37.11 |
39.4 |
36.33 |
42.0 |
| Total | 66.77 |
69.00 |
59.22 |
67.5 |
| Dependent Variable | Comparison | F | P > F |
| Bending Problems: | Student Learning Style (S vs N) | 3.20 |
.0464 ** |
| Teaching Style (S vs N) | 8.45 |
.0087 *** |
|
| Learning Style X Teaching Style | 4.08 |
.0206 ** |
|
| Non-Bending Problems: | Student Learning Style (S vs N) | 1.19 |
.3390 |
| Teaching Style (S vs N) | 0.15 |
.7006 |
|
| Learning Style X Teaching Style | 1.16 |
.3498 |
|
| Total: | Student Learning Style (S vs N) | 1.45 |
.2579 |
| Teaching Style (S vs N) | 1.19 |
.2883 |
|
| Learning Style X Teaching Style | 1.16 |
.3498 |
** Sig a = .05 --- *** Sig a = .01
While these results may initially seem to stand in contrast to the findings of Yokomoto and Ware, that is far from the case. Those authors coached individual students to overcome their weaknesses and alter their study habits. The students in this study were not coached. Instead, the presentation of lecture material was altered to favor a particular learning style. The students themselves were unaware of their own MBTI type or of the purpose of the experiment. Viewed together, these two investigations indicate that the best improvement in performance requires an active and conscious participation on the part of the student himself. Alteration of presentation mode alone is helpful but produces far less dramatic results.
In conclusion, the MBTI does appear to be useful to the classroom teachers. Its relationship to achievement is much more intricate than originally hypothesized, however. Effective use of the MBTI depends heavily upon a conscious effort on the part of the student to address his less developed dimension of the S-N continuum and upon the instructor to recognize his responsibility to develop both dimensions in all students.
The results of this investigation imply that the S-N dimension of the MBTI has important implications for teaching and learning technical material. It appears that in engineering we have an opportunity to improve the performance of students in our classrooms by recognizing the importance of individual learning styles.
Peter Rosati received the B.A. degree in engineering science from Oxford University, Oxford, England, the M.E.Sc. degree from the University of Western Ontario, Toronto, Ont., Canada, and the M.A. degree in engineering education from West Virginia University, Morgantown.
He has taught at City University, London and is currently Associate Professor in the Civil Engineering Department at the University of Western Ontario. His research activities have been focused on personalizing and individualizing the large enrollment classes in mechanics. He has designed a successful Keller-plan course in dynamics, experimented with computer problem-solving routines and is currently researching applications of the MBTI to the performance and learning styles of engineering students.
Russell K. Dean (M'79) received the B.S.E.E., M. S. M. E., and Ph.D. degrees from West Virginia University, Morgantown, in 1974, 1976, and 1981, respectively.
Since 1979 he has been a member of the Faculty in the Department of Mechanical and Aerospace Engineering, West Virginia University, where he is currently an Associate Professor and Director of Graduate Programs. During that time he has been involved in a number of educational and technical research projects. These have included study of the relative effectiveness of instructional objectives and advance organizers, multiple choice testing, and personality type as it pertains to learning style.
Dr. Dean is a member of the American Society for Engineering Education, American Society of Mechanical Engineers, Eta Kappa Nu, Tau Beta Pi, Sigma Xi, and Phi Kappa Phi. He is currently Chairman of the Professional Interest Council IV (board position) of the American Society for Engineering Education, and was the recipient of the Dow Outstanding Young Faculty Award and the 1986 Haliburton Award for Outstanding Teaching in the West Virginia University College of Engineering.
Susan M. Rodman received the B.A. degree in biology from the University of North Carolina, Greensboro, in 1965, the M.A. degree in secondary education in 1974, and the Ed.D. degree in educational psychology in 1981, both from West Virginia University, Morgantown.
In 1982, she became a member of the Faculty of the College of Education, West Virginia University, Morgantown, where she teaches courses in statistics, research methods, and computer applications In addition, she holds an appointment with the School of Medicine where she performs venous duties in biostatistics, research design, and data processing. Her research interests include the applications of the Myers-Briggs type inventory in education and the use of advance organizers in teaching technical material. She has published often in the area of engineering education and speaks frequently at meetings on that subject.
Dr. Rodman is a member of the American Society for Engineering Education.
Manuscript received August 20, 1986, revised January 11, 1988. The experimental work was supported in part with a grant from the ERM Division of ASEE.