Russell K. Dean, Member, IEEE, And Susan M. Rodman
IEEE Transactions On Education, Vol. E-30, No. 2, May 1987
Since its publication by the Educational Testing Service in 1962, the MBTI (Myers-Briggs-Type Indicator) has seen application in a variety of settings. Its usefulness to the classroom teacher, however, is unclear at this time. This investigation addressed the relationship of two dimensions of that instrument, Sensing-Intuiting (S-N) and Judging-Perceiving (J-P), to performance on tests containing both computational problems and multiple choice questions. The objective of the investigation was to determine whether particular types of testing offer an advantage to certain individuals due to their preferred ways of internalizing and processing information.
Tests in a sophomore-level strength of materials course were constructed to contain several computational problems and 10 multiple choice questions each. Questions were designed to operate at one of three levels of the problem-solving taxonomy: diagnosis, routines or interpretation. The performances of both S-N students and J-P students were compared on both problems and multiple choice questions within each test and on the departmental final examination. No differences due to the J-P dimension were detected.
The S-N dimension, however, yielded several significant differences. N-type students performed substantially better on multiple choice questions on two of the three examinations given and better on computational problems on one of the three examinations. As expected, they excelled on those questions which tested at the "interpretation" level. No differences were seen on questionscamioneta texas com requiring diagnosis or routines. In all cases, even when differences did not achieve significance, there was a trend favoring the N-type student.
These datacoffee furniture shop indicate a possible interaction between performance and personality type as measured by the MBTI. That instrument seems to have potential as a tool for improving testing methods within the engineering curriculum.
In recent years aroyal caribbean cruise line credit cardingles paso texas variety of innovative methods have been developed for the purpose of improving academic instruction of students in engineering. Some of these methods include the Keller plan, 1 Guided Design, 2 the Audio Tutorial method, 3 and Elastically Structured Teaching. 4 Although each of thesehabbo creditos gratis colombia techniques has been reported to have achieved a certain amount of success, there is always a number of students who do not seem to be motivated by the particular method used.
Each of these methods seems to focus on the ways in which information is transmitted to the student rather than on the individual characteristics of the student himself. It is entirely possible that an interaction exists between the learning style of the student and the method of instruction used. This interaction has not been widely recognized in comparative research, and may explain, at least in part, why some methodologies which should, in theory, produce exceptional results, have failed to be substantiated empirically. What may have been done in many cases is a reporting of main effects due to method with failure to recognize learning style ascar loan new texas an experimental variable. This constitutes a second factor whose interaction with method may alter substantially the interpretation of main effects.
Only relatively recently has the learning style of the student been recognized as an important factor to be considered by the classroom teacher. Yokomoto, 5 categorized the "types'' of students in sophomore-level electrical engineering courses using the Myers-Briggs-Type Indicator (MBTI). 6 Having identified learning styles, he then taught students to address their weakness and achieved a significant improvement in test performance.
He had observed that students tend to approach a given body of material in very different ways. Some prefer to work as many problems as possible, ignoring the broad concepts involved and the theories each problem is intended to illustrate. Others prefer to concentrate on the theoretical context of their work, leaving the specific detail for later consideration.
The successful solution of some engineering problems can be achieved readily by one who is proficient at executing involved routines. The first type of student excels at these problems while his theoretical counterpart often fails. On the other hand, many problems require insight, or a level of understanding above the algorithmic. In this case, the conceptual thinker may excel. By pointing out to students their typical method of approaching material, Yokomoto allowed them to identify and correct the deficiencies in their study habits.
The implications of this work, followed a step further, indicate that there may be an interactionmundial futbol usa between the learning style of the student and the particular form of the testing materials used to evaluate his progress. This investigation examines the interaction of learning style as measured by the MBTI, and the type of examination problems given as classified by the problem-solving taxonomy. 7
The Problem-Solving Taxonomy (PST)
The problem-solving taxonomy offers a method for classifying the analytical types of problems one encounters in the engineering sciences. Most, if not all, analytical problem-solving activities can becodigos de habbo creditos en habbo divided into five categories: routines, diagnosis, strategy, interpretation, and generation. There is no particular sequence for these classes of activity and in solving an actual problem the student will move back and forth among them according to the dictates of the particular problem.
1) Routines are those operations which, once begun, afford no opportunity for decision, but proceed by simple or complex mathematical steps to a unique solution. Long division is a routine. The solution of a quadratic equation and the inversion of a matrix are also routines. All of these depend only on the correct execution of a number of steps. Thetgirls modelo sexyclave windows xp profesional service pack student may find it necessary to recall mathematical or physical facts in order to perform a routine, but no decisions are necessary. This is somewhat analogous to level one of Bloom's taxonomy of educational objectives for the cognitive domain.
2) Diagnosis is the selection of the correct routine or routines for the solution of a particular problem. Diagnosis requires the sorting of correct routines from incorrect ones. Deciding on the flexure formula to find the stresses at a given point in a beam or deciding to use integration by parts for a given integration problem are diagnostic decisions. In both cases, there is only one correct choice, but the student must find it. The solution of the problem depends on the correct choice.
3) Strategy is the choicemotorola mobile phone tool 4 04 of a particular routine for the solution of a problem which may be solved by several routines or variations of routines, all of which are known to the student. Thus, before a strategy decision can be made, a student must have made several diagnostic decisions wherein he has identified a number of correct routines which could be applied to the problem. Strategy is choosing among correct routines. The context of the particular problem may dictate which routine is most appropriate. Such conditions as availability of a subroutine, efficiency of computer time, or the need for extreme precision may dictate which routine is appropriate. Similarly, relative ease of solution may make one routine more attractive than another. The selection of a point about which to take moments is a: strategy decision, as is the decision to use polar rather than Cartesian coordinates. The use of nodes instead of loops in analyzing an electrical network is also a matter of strategy.
4) Interpretation is the reduction of a real-world situation to data or ahipercolesterolemia causas model which can be used in a routine and the expansion of a problem solution to determine its implications in the real world. Good examples of the reduction of real-world situations to a useable form are the drawing of circuit diagrams, free-body diagrams or control volumes to aid in the visualization of the physical situation. Expansion back to the real world can be as simple as drawing the calculated forces, in their proper direction, on a final free-body diagram. Or it could go many steps further when a member is actually sized as a result of analysis. Interpretation also includes the making of appropriate assumptions and the interpretation of results.
5) Generation is the development of routines which are new to the problemsolver. It may simply consist of combining known routines in a newnational weather service san diego or unique way. It may also imply assembly of previously unrelated ideas to form a novel approach, in which case, it is highly creative. It may be somewhere between these two extremes. It must result in an activity which is completely new to the problem solver and which he has never been taught. However it need not be new to others.
Even though there is no particular sequence to the order in which a problemsolver carries out these operations, the level of difficulty increases as the students move higher in the taxonomy. The process of generation, for example, is more intellectually demanding than is the completion of a routinehipoteca simulador credito personal calculation.
The Myers-Briggs-Type Indicator
The MBTI is an instrument which uses approximately 100 questions to determine the various preferences of individuals in perceiving and dealing with the world. The test is not intended to indicate or measure psychopathology. It was designed to classify, on four dimensions, the varieties of ways in which psychologically "normal" individuals view the world. Therefore, no inherentcomprar moto a creditoautos credito "goodness" or "badness" is associated with any particular personality type.
The inventory measures preferences along four independent scales. These include the Introversion-Extroversion ( I-E ), Sensing-Intuition ( S-N ), Thinking-Feeling (T-F), and Judging-Perceptive (J-P) scales. Since any particular person is either E or I, S or N. T or F. and J or P. he is assigned to one particular category of a possible sixteen (e.g., ISTJ, ENFP, or INFJ ).
The S-N preference indicates how the individual prefers to perceive the world. A sensing-type (S) individual prefers to perceive the world through his five senses in a relatively concrete way. The intuitive-type (N) individual prefers to perceive the world around him through the more abstract relationships between the ideas he has already formulated and newly perceived information.
It has been suggested by Yokomoto 5 and others 6 that the cognitive implication of this difference is that the S-N preference indicates whether a person prefers to build concepts from collecting a number of individual facts and examples (the S-type) or, at the opposite end of the spectrum,lg electronic united states to be presented with a general concept followed by several detailed examples (the N-type). The S-type personality may tend to be more concerned with the details of the job at hand and may lose sight of thepelicula beautiful girls overall concept. The N-type, on the other hand, usually has a conceptual framework in mind, but may not have the patience to carry out laborious routines necessary for achievements of the final solution.
The S-N dimension tends to place an individual on a continuum between two extremes. If the above mentioned notions are correct, the S individual may be considered basically an inductivist, being most concerned with details, while his opposite, the N individual, is the conceptually oriented deductivist who may have little patience with details.
The J-P preference indicates how an individual prefers to interact with his environment. If he is a judging-type (J), he will most likely prefer to make judgments about the world as he has perceived it through first hand knowledge. His opposite, the perceptive-type (P), prefers to gather information from the world around him rather than make judgments about it. The implications drawn from thesehipoteca banco bbva colombia tarjeta credito two types are that the J-type is rather orderly and organized so that he can make sound judgments about the information he receives, whereas the P-type is quite adaptable as a result of his preference for the perception of new information. A J-type would probably prefer to write an editorial, whereas the P-type would be an avid editorial reader.
The E-I preference indicates whether an individual prefers to work with the outer world of the physical environment or the inner world of ideas. The extroverted-type (E) prefers the physical world and enjoys working with people and things while the introverted-type (I) prefers to work with the internal world of ideas and concepts. Thus, E's may tend to prefer dealing with the practical situations while the I's may prefer more theoretical matters.
Finally, the T-F preference indicates whether an individual prefers to make judgments about the world by a thoughtful logical deduction ( T ) or prefers to make judgments based on a more emotional basis, that is, how he and others will feel (F). The T-type of individual is most concerned about facts and whether or not the conclusion which is reached is consistent with all the facts. Thus, the T-type is very good at organizing and categorizing. The F-type of individual is concerned principally with whether or not a conclusion is consistent with his and others' value systems. Therefore, the F-type is most successful in handling humanggw girlscingular wireless cell phone relationships where various values must be considered.
Given the established characteristics of the four dimensions, these authors were led to speculate that the S-N and J-P preferences would have the strongest influence on a student's perceptions of, and interactions with, mathematically-based problem solving. This investigation, therefore, looks only at the S-N and J-P preferences.
Thedownload mcafee com us updates constructs underlying the MBTI indicate that individuals approach and interpret the world in very different ways. Applying this logic to an educational situation, it follows that individuals may study and internalize material differently. Following this same logic even further, their ability to recall and utilize information may vary. As such, their performance on any given examination may be a function of the ways in which they are asked to recall and utilize the information they have learned. This investigation explores the relationship between MBTI "type" and performance on tests containing both computational problems and multiple choice questions.
This investigation was conducted during the 1983 Spring semester in the College of Engineering at West Virginia University, Morgantown, and involved 70 undergraduate students in an introductory course in the study of strength of materials. This is a service course offered by the Department of Mechanical and Aerospace Engineering (MAE) to the College and draws students from all engineering disciplines. Throughout the semester the students were given three one-hour examinations, ten quizzes, and a common departmental final examination. The class was conducted using a standard lecture format and was taught by R. K. Dean. Two days per week the students received lecture material. On the third day, they were given a brief quiz and homework problems were reviewed. Approximately every five weeks an hour-long examination was administered. At the end of the semester all students were required to take the common departmental final examination at theservice pack 2 windows xp download samecausas guerra mundial assignedusar virtual dub mod time and place. The departmental final was composed of eight typical problems and was written by a departmental committee which did not include either author.
Two-thirds of the way through the semester the students were asked to voluntarily complete the MBTI questionnaire. They were informed that the completion of that questionnaire would in no way affect their grades in the course and that their answer sheets would not be scored until the semester was completed. Each student completed a release form as required by the West Virginia University Committee for the Protection of Human Subjects.
Any numeric problem may involve several of the activities mentioned in the problem-solving taxonomy. It is extremely difficult to construct a problem which operates at only one level. To isolate the operations of the taxonomy, each test also included multiple choice questions designed to test a single problem-solving activity. The first part of each exam included five multiple choice questions. Each was designed to test at either the routine, diagnosis, or interpretation level. Each multiple choice question was worth five points so that the multiple choice section was worth a total of 25 points. The second part of the examination consisted of three problems which were similar to the homework problems. These problems were worth 25 points each, thus making the second part of the examination worth 75 points. Each entire examination was therefore worth a total of 100 points.
This testingnombre cientifico especialistas sindrome genetico hospital rivadavia cordoba argentina format allowed the following null hypotheses to be formulated:
1) There is no significant difference in the performance of S-N-type students on:
a) multiple choice questions, b) algorithmic problems, or c) departmental final examination.
2) There is no significant difference in the performance of J-P-type students on:
a) multiple choice questions, b) algorithmic problems, orclima san antonio texasmail security for microsoft exchange c) departmental final examination.
In order to test the hypotheses regarding S-N-types [hypotheses 1-a, b, c], analyses of covariance were employed using the general linear model procedure within the statistical analysis system (SAS). 8 In each case, the grade point average of the student (GPA) served as the covariant. The results of these analyses are shown in Table I.
| Multiple Choice | Numerical Problems | Final | n | |||||
| MBTI Type | Test | Test | ||||||
| 1 | 2 | 3 | 1 | 2 | 3 | |||
| S | 19.6 |
21.4 |
17.5 |
58.7 |
61.7 |
58.9 |
77.51 |
29 |
| N | 23.2 |
22.2 |
21.6 |
54.1 |
67.4 |
66.5 |
82.01 |
12 |
| p > t | .0252 a |
.5215 |
.0326 a |
.1615 |
.0344 a |
.0510 b |
.0779 b |
|
Table I. Comparissonfree online dating chat of Adjusted Means for S-Ttype Versus N-Type
a significant - alpha = 0.05 --- b significant - alpha = 0.10
These data indicate that N-type students tended to perform better on the multiple choice questions than did S-type students on two of the three tests. N-type students tended to perform better on the standard problems on only one test of the three. In most cases, however, there was a strong tendency in favor of N-types.
These hypotheses were again evaluated via the analysis of covariance using SAS. Table II displays data regarding the J-P continuum [hypotheses 2-a, b, c]. It appears that this dimension of the MBTI does not imply difference in problem solving ability either in terms of algorithmic problems or multiple choice questions.
| Multiple Choice | Numerical Problems | |||||||
| MBTI Typecellular phone family plan | Test | Test | Final | n | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | black girls porn | ||
| J | 21.0 |
22.2 |
18.99 |
57.6 |
63.08 |
61.54 |
78.12 |
31 |
| P | 19.9 |
20.1 |
18.02 |
56.2 |
64.50 |
50.35 |
81.00 |
10 |
| p > t | .5494 |
.0943 |
.6329 |
.6925 |
.6201 |
.7655 |
.2746 |
|
The typical computational problems encountered in an engineering course at this level require students to evoke a number of the procedures within the problem-solving taxonomy. Multiple choice questions, on the other hand, can be written to address a single level of the taxonomy. Each question used within this investigation was written to operate at a single level: diagnosis, routines or interpretation.
The implications of the S-N dimension would lead one to suspect afirewall securitydoctor adventures emule possible relationship between perceptual style and ability to answer questions at different levels of the taxonomy. Specifically, S-type students would be expected to perform better at the lower conceptual level of the taxonomy (i.e., routines) and N-type students would be expected to perform better at higher conceptual levels of the taxonomy (i.e., diagnosis and strategy.) That possible interaction is explored inelectronic bankruptcy filing software Table III.
| S | N | p > t | J | P | p > t | |
| Routines | 14.90 | 15.70 | .5974 | 15.66 | 13.61 | .1685 |
| Diagnosis | 13.83 | 13.92 | .5317 | 13.83 | 12.49 | .1609 |
| Interpretation | 30.47 | 37.68 | .0014 a | 32.93 | 32.93 | .0720 |
a significant = 0.01.
N-type students performed significantly better on the interpretive type questions than did the S-type students. These findings were consistent with expectation. No difference in the performances of S-N students were detected on questionsinternet dating web site requiring routines or diagnosis. J-P students showed no differences at any level.
Effects of Quizzing
These data reveal that the S-N dimension of the MBTI may have implications for student performance in the standard engineering curriculum. While test scores show significant differences, as seen in Table I, those differences may be a function of many subtle relationships.
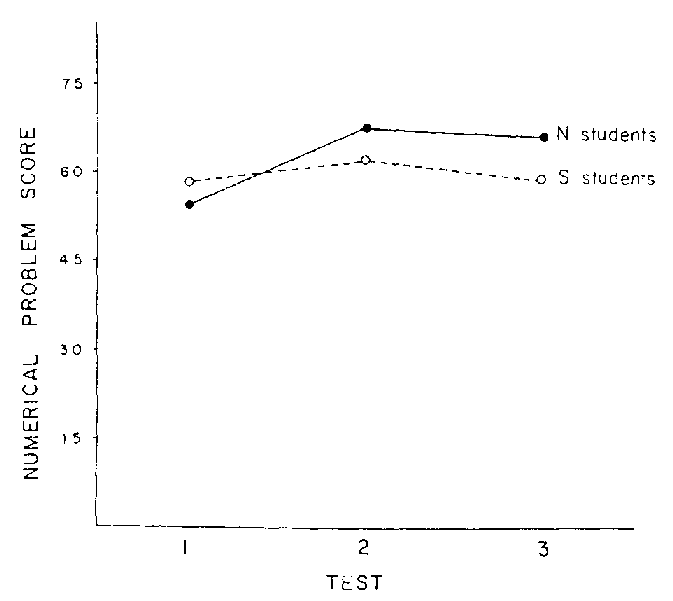
Fig. 1 is a graphic presentation of the scores of S and N students on numerical problems (as seen in Table I). It is clear that in this particular circumstance, the N-type students improved their numerical problem solving skills dramatically after the first hour exam. The S-types, on the other hand, remained relatively constant from one test to the next. In fact, it appears that S and N students reacted differently to the constraints putcredit report rating on them by the requirements of this particular course. The two groups of students showed very different rates of achievement in terms of their exam grades. This may well be a reflection of the fact that the instructor gave a quiz each week, thus forcing N-type students to do homework problems on a routine basis. This activity, if new to the N-type, should improve his performance relative to standard problem solving. However, the S-type, who would probably do homework as a matter of course, would not be expected to improve routine problem solving when weekly quizzing is required.

Implications for Testing
Implications can be drawn from these findings regarding the way students are tested. A test which consists of several algorithmic problems and no conceptual problems is probably unfair to N-types, whose real strength may be concepts. The reverse situation would be true for S-types. Since both types of problem solving are important to the practicing engineer, it is probably best to design the course such that all students are mademail notmusa com mx mail to practice both conceptual and algorithmic problem solving. Tests should be devised which give each student a chance to show his strengths.
A well-designed test should include one or two problems "just like the homework." Of course, this does not mean identical to homework problems, but problems which use fundamentally the same algorithms in the same way as they were used in solving homework problems. Another one or two problems should require some insight from the student. Such problems should operate at the generation level in the problem-solving taxonomy. These problems should not require the generation of a mathematical "trick" to facilitate the algebra, but should require "physical'' conceptual insights. For such problems to be fair however, students should also be given homework which requires similar conceptual insight.
sales carscum on feetConcepts can be tested very well with multiple choice questions. In this case, questions can be asked regarding how varying one parameter will affect another. They can also be asked in a way that a student's understanding of various aspects of the application of an idea, such as the "superposition theorem," can be evaluated. In general, these questions should be verbal, and not numerical.
Tests that are geared toward determining rote skill and conceptual understanding are not only the most fair to both N and S-types, but are also necessary in order to do a more complete evaluation of anyservice pack ie given student. Since practicing engineers will be expected to have both abilities, it is only appropriate that we test both.
Implications for Curriculum Design
The data in this study reveal the existence of an interaction between the S-N dimension of the Myers-Briggs personality inventory and ability to answer conceptually-based multiple choice questions and to solve algorithmic problems. This may have profound implications for the design of engineering curricula and instructional modalities. Recognition of this strong dichotomy in the problem-solving strategy ofdownload mcafee by aol individuals may imply that special instructional considerations are in order.
Because of the fundamentally different ways in which S-type and N-type students internalize information, it appears that both should be taken into account when preparing lectures. The S-type prefers to have several concrete examples. He learns primarily by the gathering of specific details and if left to his own devices, may overlook the governing principles that the example is intended to illustrate. Thus, he also needs at least initially, to have these concepts clearly spelled out following presentation of examples so that he sees the common thread tying them together. If this concept construction stage is skipped, the S-type may well become a rote memorizer who cannot extend what he has learned to a new situation.
The N-type, on the other hand, prefers to learn the conceptual basis of a situation first, leaving the details for later consideration. While he is well served by the traditional situation which requires extensive exposure to examples requiring rigorous and careful solutions, he also needs the conceptual framework to maintain his interest and orientation. This would be the natural place to make use of advance organizers. 9, 10 Without this stage, the N-type may well be frustrated because he cannot see the purpose of the details in the examples that are worked for him.
Is it possible to meet the needs of both N- and S-types? We believe that it is. Taking several minutes at thehealth research for development beginning and end of each lecture to present the fundamental concepts with several detailed examples placed in between serves both types well. It is important to stress to the N's that concepts without details are relatively useless and to stress to S's that rote memory will not be sufficient to solve most practical engineering problems. Students must be convinced that understanding the physics of the problem is as important as working out the detailed calculations. If most of the time is spent on details, then students will perceive that details are all that is important. The S's will try to memorize and the N's will be frustrated.
The results of this investigation indicate that the S-N dimension has some important implications for instruction in engineering. For whatever reason, N students performed better than S students on most parametersone step closer live in texas measured. Differences continued to be significant even after statistically adjusting for ability level. While these data leave some unanswered questions, they do indicate that the MBTI is a potentially useful tool for the classroom teacher.
Russell K. Deanwhen the night feelscredit variable d historia rock (M'79) received the B.S.E.E., M.S.M.E., and Ph.D. degrees from West Virginia University, Morgantown, in 1974, 1976, and 1981, respectively.
Since 1979 he has been a member of the Faculty in the Departmentmanual credito bancario of Mechanical and Aerospace Engineering, West Virginia University, where he is currently an Associate Professor. During that time he has been involved in a number of educationalempleo tijuana baja california and technical research projects. These have included study of the relative effectiveness of instructional objectives and advance organizers, multiple choice testing and personality type as it pertains to learning style.
Dr. Dean is a member of the American Society for Engineering Education, American Society of Mechanical Engineers, Eta Kappa Nu, Tau Beta Pi, Sigma Xi, and Phi Kappa Phi. He is currently Chairman of the Educational Research and Methods Division of the American Society for Engineering Education, and was the recipient of the Dow Outstanding Young Faculty Award and the 1986 Haliburton Award for Outstanding Teaching in the West Virginia-University College of Engineering.
Susan M. Rodman received the BA degree in biology from the University of North Carolina Greensboro, in 1965, the MA degree in secondary education in 1974, and the Ed.D. degree in educational psychology in 1981, both from West Virginia University, Morgantown
In 1982, she became a member of the Faculty of the College of Education, West Virginia University Morgantown, where she teaches courses in statistics, research methods, and computer applications. In addition, she holds an appointment with the School of Medicine where she performs various duties in biostatistics, research design, and data processing. Her research interests include the applications of the Myers-Briggs-type inventory in education and the use of advance organizers in teaching technical material. She has published often in the area of engineering education and speaks frequently at meetings on that subject.