Charles E. Wales, Assistant Professor Of Chemical Engineering, Purdue University
Engineering Education, February 1967
Engineering educators have been challenged to correct a weakness in the teaching of engineers. One of the many people who have identified this weakness is Eric Walker, President, The Pennsylvania State University, who said in a speech: "the teachers of engineers have never found a really satisfactory way of preparing their students for the kind of creative activity that should be the engineer's principal concern."
Interpreting this criticism, engineering education should have two objectives: to increase each student's knowledge and to develop each student's wisdom. Knowledge and wisdom, the key words in this statement, are defined as follows:
In most of today's classrooms, the emphasis is primarily on knowledge. This is not surprising, because knowledge is growing at a fantastic rate. However, each new fact added to the curriculum correspondingly reduces the time available for developing wisdom. This change does not seem to bother most teachers, for wisdom was never easy to teach and always difficult to evaluate. By contrast, knowledge is easily transmitted through lectures and reading assignments, and the knowledge a student has acquired is easily evaluated by an objective examination.
Unfortunately, this primary emphasis on knowledge has distorted the student's attitude toward higher education. Knowledge is no longer an ally that helps solve problems; instead, it has become the student's enemy, to be memorized and conquered. Students no longer look forward to each class meeting as an intellectual challenge. Today's students say, "Where did you go? Class! What did you learn? Nothing!"
To further complicate matters scientists warn that the knowledge explosion will make obsolete tomorrow much of what the student learns today. Engineers voice a similar warning that technology is changing rapidly and that what the student learns today may not be applicable in tomorrow's industry.
If today's students are to succeed in tomorrow's world, they must understand that knowledge is only a raw material and that wisdom is the tool that makes the raw material useful. As it is impossible to equip each student with a life-time supply of knowledge, why do engineering teachers try to do it? Would it not be better to teach students how to search for knowledge, where to search for knowledge, and how to use the knowledge they find?
If Dr. Walker's criticism is justified, if engineering education should include both knowledge and wisdom, then engineering educators must develop new teaching methods that will achieve both objectives. The tools required to do these jobs are available now. Described here is a very promising method of using these tools to meet the challenge. In summary, this article tells how principles of educational psychology can be used to design an engineering course; how programmed instruction can be used to teach basic knowledge and wisdom outside of class, how these programs are prepared, and the results of my research with programs; and how classroom work can be used to teach engineering students to think like engineers.
The first step in this new design is to identify specific knowledge objectives. Below is an example of some of the specific knowledge objectives a teacher should prepare for the ideal gas law.
At the end of this period of study, each student should be able to:
- the van der Waal equation.
- the compressibility factor equation.
A set of knowledge objectives is not the kind of syllabus common to most engineering courses. It is not just a week by week or day by day topic outline. Each knowledge objective states one task the student should be able to perform. This is a list of student behaviors and includes active verbs, such as write, define, predict, solve, and analyze.
Some engineering educators will react to this list with thoughts such as: "Who needs it?" or "that's busy work for high school teachers, not college teachers." They are wrong. This list has a very sound psychological basis. To prepare this list, the teacher will be forced to analyze the subject to a new depth. In building and expanding the list, the teacher discovers new and more logical methods of organizing and presenting the material. If a set of knowledge objectives is written for one concept it is planned to teach, it will be discovered that this list is an important first step toward effective teaching.
The completed list of knowledge objectives establishes what it is expected that each student know and how he is expected to demonstrate his knowledge. Now, what about wisdom? What are the wisdom objectives and how are they related to this list? Educational psychologists have structured wisdom objectives into seven different levels, the first three levels of which are recall, comprehension, and application. These three wisdom objectives are used to organize and integrate the knowledge objectives into a learning experience. This is illustrated by a set of questions about the ideal gas law.
Chemical engineers are frequently concerned with calculating the volume occupied by a certain quantity of a gas. The volume (V) of a real gas is a very complex function of both its pressure (P) and temperature (T). This function can be approximated by fitting a multi-term equation to experimental data points but such equations are used in only the most exact calculations. The volume of a real gas can be approximated by assuming that it behaves like an ideal gas. The pressure, volume, quantity, and temperature of an ideal gas are related by the simple equation:
PV = nRT
where:
P = the pressure (atm)
V = the volume of n moles (cu-ft.)
n = the number of moles of gas (lb-moles)
R = the gas law constant (0.73 atm-cu-ft./lb-mole-°R)
T = the absolute temperature (°R)
1Q. To calculate the volume of an ideal gas you must know the value of R, and specify the values of the other variables, __, __, and __.
2Q. A given quantity of an ideal gas is contained in a cylinder; if the temperature is held constant while the pressure is doubled, the final volume will be __ the original volume.
3Q. One lb. mole of a gas is compressed to 30 atm. The temperature is 1000 °R; the volume is 24.3 cu. ft. Does this gas obey the ideal gas law at 30 atm.?
4Q. The temperature outside is zero degrees Fahrenheit (460 °R), but that doesn't stop a meteorologist and his crew who are outside preparing to launch their weather balloon. They have just filled the balloon with 500 cu. ft. of hydrogen gas. The empty balloon and its equipment weigh 25 lbs. How many 175 lb crew men will it take to hold the inflated balloon down?
This learning experience consists of the following parts:
1. An information paragraph based on items from a list of specific knowledge objectives.
2. A question which restates some of the key facts and omits others. By completing the sentence, the student will demonstrate his ability to recall these key facts.
3. A question which requires the student to demonstrate his comprehension of the concept by making use of it in one of the following ways:
(a) by identifying an example of the concept.
(b) by identifying the concept after it has been translated into a new symbolic form, or by performing the translation.
(c) by using the concept to interpret data or to predict trends or consequences.
4. A question that requires the student to use the concept to solve a problem. (Direct application)
5. A question that requires the student to analyze a problem statement to determine that the concept applies before he uses the concept to solve for the answer. (Indirect application)
A complete learning experience is undoubtedly more involved than this simple example, but these steps are basic to an effective learning experience. A teacher could use this set of questions as the basis for his classroom presentation. But, by simply adding the answer to each question, this work can be converted into a programmed lesson, as shown below.
1Q. To calculate the volume of an ideal gas you must know the value of R, and specify the values of the other variables,___ , __, and ___.
1A. P, T, and n.
2Q. A given quantity of an ideal gas is contained in a cylinder; if the temperature is held constant while the pressure is doubled, the final volume will be the original volume.
2A. 1/2 the original volume.
3Q. One lb. mole of a gas is compressed to 30 atm. The temperature is 1000øR, the volume is 24.3 cu. ft. Does this gas obey the ideal gas law at 30 atm.?
3A.V = nRT / P
= (1 lb-mole)[(0.73 atm-cu ft/ lb-mole-°R)(1000 °R / 30 atm)
= 24.3 cu. ft.
Answer Yes. it does obey the ideal gas law.
4Q. The temperature outside is zero degrees Fahrenheit (460 °R), but that doesn't stop a meteorologist and his crew who are outside preparing to launch their weather balloon. They have just filled the balloon with 500 cu. ft. of hydrogen gas. The empty balloon and its equipment weigh 25 lbs. How many 175 lb. crew men will it take to hold the inflated balloon down?
4A. This problem is solved by evaluating two forces:
1) The force downward: The weight of the balloon, its equipment and the hydrogen gas. The balloon and its equipment weigh 25 lbs. If H2 behaves as an ideal gas it weighs:
wt. = n x mol. wt. = PV/RT ( mol. wt. )
n x (2 lb / 1 lb-mole) = [(1 atm.)(500 cu. ft) / (0.73)(460 °R)] (2) = 2.98 lb.
2) The force upward the buoyant effect of the air which is displaced by the balloon (Archimedes Principle). The weight of the 500 cu. ft. of displaced air is the force upward. If air behaves as an ideal gas, it weighs:
n x (29 lb / 1 lb-mole) = [(1atm.)(500 cu. ft.) / (0.73)(460 °R)] (29) = 43.2 lb.
The net force upward is: 43.2 - (25 + 2.98) = 15.22 1b. One 175 lb man can hold the balloon down.
There is no reason to use class time to present this programmed material. The students can study these questions and answers outside of class. Studying with the program, students can be expected to learn more, learn faster, and retain more than students taught in the conventional manner. Programmed lessons are more effective teachers than books or lectures, because programs are designed to achieve specific knowledge and specific wisdom objectives while textbooks and lectures are usually not designed on this basis. Each question in the program can be, and usually is, pre-tested on individual students to be sure it is clearly written and does the job it is designed to do. With a program, the student can work at his own rate; his teacher is neither too fast nor too slow. If he has trouble with a concept, he can repeat that portion of the work as often as necessary. The student is actively involved with each question and each answer. He is not trying to listen and take notes at the same time. The student is reinforced at each step by the correct answer. In addition, he can examine the step-by-step logic used by the instructor to develop each concept.
Programmed learning is based on a set of sound psychological principles. Is there any reason to doubt its superiority over other methods of instruction? My own programs, which consist of about 400 questions and answers, were written before developing the plan described here, but experiments with these programs convinced me of their value. These programs were used in an experiment in a sophomore class in Chemical Engineering Calculations in the fall of 1963. One class took the programs home as a supplement to their regular work; the control class had none. Both classes had the same homework assignments, and both took the same examinations in a special evening period. Each class period was devoted to a lecture-discussion of the material contained in the program. The control class took notes in the regular manner. However, the program class soon learned that they could depend on the program to fill in lecture gaps and I had their undivided attention. As a result, we were able to explore the problems more fully. It was not unusual for this class to leave the main path and explore the side roads. By studying the program at home, they were always able to learn any material that had not been covered in class. It was this experience that convinced me that programmed instruction can be used to teach both knowledge and wisdom objectives outside of class.
Student reaction to the programs is very encouraging. Perhaps student response alone is sufficient to justify the use of programmed instruction, because the students are happy to put forth the extra effort required by the programs.
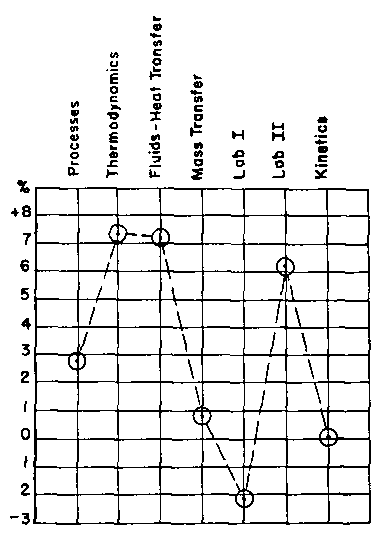
What about grades? Did an eight-week exposure to the programs have any effect on the students' grades? Yes, the program class scored 7% above the control class on the first examination. However, subsequent examinations for non-program areas of the course produced equally great differences, so no great case for programmed instruction can be built on this score. What about grades in subsequent chemical engineering courses? Did eight weeks of work with programmed instruction have any effect on the students' performance after they were mixed with the control class in the regular course sequence? The data are shown in Figure 1, where the performance of the program class in each subsequent chemical engineering course is compared to the performance of the control class. The average grade of the students from the program class is higher than that of the control class in all courses except Laboratory I. The greatest difference occurred in thermodynamics, where the program students scored an average of over 7% higher than the control students. However, this difference is at least in part due to the fact that the students who used the program have a cumulative grade index that is approximately 1% higher than the control students. A dotted line shows the expected level of performance of the program class at this 1 % level.

A comparison of the average of chemical engineering grades and the average of university grades shows that an average grade in a given chemical engineering course might vary by as much as 4.5% from the expected level. This qualification reduces the number of significant grade differences to three; the program students outperformed the control students in Thermodynamics, Fluid Flow-Heat Transfer, and Chemical Engineering Laboratory II.
A revised and expanded set of programs was used in a second experiment in the fall of 1965. Here again I taught two classes of Chemical Engineering Calculations.
In this experiment, both classes used a program as a supplement to the regular material for the first section of the course; only one class used the second program; the other class used the third program; etc. Neither class had a program for the final section of material. Both classes took the same examinations in a special evening period.
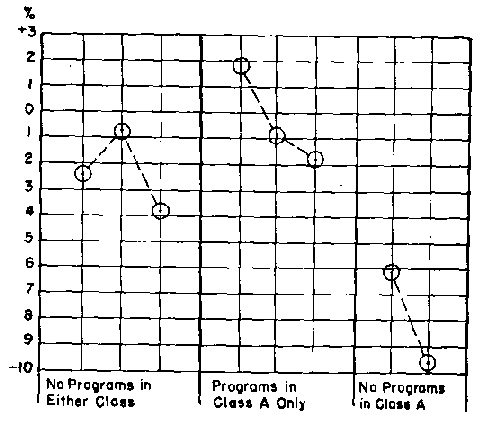
Previous university grades indicate that class A (80.3% ) can be expected to score 2.9% below class B (83.2% ). Figure 2 shows the actual performance of class A compared to class B. When both classes used a program and when neither class used a program, class A scored near their expected level, 2.9% below class B. When class A used the program and class B did not, class A performed consistently several percent above their expected level. When class A did not use the program, they performed several percent below their expected level.
Is programmed instruction an effective teaching aid? This research supports the conclusion that it is. This comes as no particular surprise, because programmed learning is a logical extension of the teaching process.
The next question is, Do good programs exist? Unfortunately, they do not. Very few college level programs have been written, and very few engineering programs exist. Teachers have been using class time to do what the program can do outside of class. As soon as good programs are prepared, engineering educators can begin to use class time to do what they have been criticized for neglecting: teaching students to think, teaching students to use the highest levels of wisdom, creativeness, analysis, synthesis, and evaluation. These four wisdom objectives should be the objectives of all courses taught. They can be developed through the use of case problems. For example, this is the kind of problem the students in an engineering class should explore:
Concentrated sulfuric acid is shipped in railroad tank cars that have a capacity of 50 tons of acid. Design a system to transfer the acid from the tank cars to a chemical plant.
This is a case problem. To solve it the student must analyze, synthesize, and evaluate. Each of these steps will involve a degree of creativeness; each of these steps will require the student to produce something that is new to him. To identify the important elements of the problem statement, the student must ask questions; he must analyze. In addition to the elements, he should identify the tools or methods which might be used in a solution of the problem. Synthesis is required when the student attempts to identify the specific components which can be used and when he begins to assemble these components into a design.
Evaluation must be performed at every step. The student must identify the standards he will use in the evaluation; he must identify the elements important enough to be evaluated. If two designs are produced, he must evaluate and choose between them.
It is certainly not obvious from the problem statement that one of the best solutions involves the ideal gas law. The sulfuric acid can be removed from the car by forcing compressed air into the car. This case problem shows the student how the ideal gas law he has studied can be used as a tool to solve a real problem. Through a combination of programmed instruction and classroom work, the teacher has not only transmitted knowledge about the law but has also helped the student gain wisdom about using the law. The ability to think is timeless. Creativeness, analysis, synthesis and evaluation can be applied equally well to today's problems, using today's knowledge, and to tomorrow's problems, using knowledge that has yet to be discovered. An engineering education that uses the best current knowledge as a vehicle to develop each student's wisdom can never be less than the best education. This is education to meet the challenge of the future.